IEEE754浮点标准
2022-03-01
一、基本结构
浮点系统采用位模式来表示数值。一个数值的表示由3部分组成：符号位（S)、阶码（E)和尾数（M)。每个（S，E，M)模式根据下列格式可以标识一个唯一的数值：
\[value = (-1)^S\times1.M\times{2^{E-bias}}\]S的含义最简单，0表示正数，1表示负数。
E和M的含义要复杂的多。
下面的示例中，假设一个浮点数包含1位符号位，3位阶码和两位尾数。
二、M
1.M是标准要求的形式，这使得对于每个浮点数而言，它的尾数是唯一的。
满足这种限制条件的数称之为规格化数（Normalized Numbers）。
实际中，前面的1是可以省略的，因为这是约定俗成的。
举例来说，0.5D允许的唯一尾数是M=0.
$0.5D = 1.0B \times 2^{-1}$
D表示10进制，B表示二进制。
据此，m位的尾数就可以有效表示（m+1)位尾数的值。
三、E
用于表示E的位数决定了数的表示范围。
比较复杂的是E的表示方法。
首先补充一点正码、反码和补码的基础知识。
原码
将一个整数，转换成二进制，就是其原码。
如单字节的5的原码为：0000 0101；-5的原码为1000 0101。
反码
正数的反码就是其原码；负数的反码是将原码中，除符号位以外，每一位取反。
如单字节的5的反码为：0000 0101；-5的反码为1111 1010。
补码
正数的补码就是其原码；负数的反码+1就是补码。
如单字节的5的补码为：0000 0101；-5的原码为1111 1011。
余码 在e位的表示系统中，补码加上($2^{e-1}-1$)就构成它的余码表示法。 余码表示法的好处是无符号比较器可以用来比较有符号数。
实际标准中，E就是用余码表示的。
假设E用三位表示，那么它可以表示的范围是-3到+3。 当把它的余码表示看做无符号数时，发现也是单调递增的。
如下表所示：
| 二进制补码 | 十进制值 | 余码 |
|---|---|---|
| 101 | -3 | 000 |
| 110 | -2 | 001 |
| 111 | -1 | 010 |
| 000 | -0 | 011 |
| 001 | 1 | 100 |
| 010 | 2 | 101 |
| 011 | 3 | 110 |
| 100 | 保留模式 | 111 |
留心观察会看到，余码表示法中，尾数为0表示奇数，尾数为1，表示偶数。
四、举例说明
用6位的格式来表示0.5D.
0.5D=0 010 00
其中，S=0，E=010， M=（1.）00
n = 3
具体计算过程如下：
\[\begin{split} 原式&=(-1)^0\times 1.00B\times2^{010B-(2^{(3-1)}-1)D} \\ &= 1 \times 1B \times 2^{010B-011B} \\ &= 1 \times 1B \times 2^{101B} \\ &= 1 \times 1D \times 2^{-1D} \\ &= 0.5D \end{split}\]这里有两个容易混淆的地方，第一个，就是E是用余码表示的，总想把它还原成原码，这是不用的。直接将E和bias都看做一个无符号数进行相减，得到的数当做原码表示就可以了。
第二个，就是二进制和十进制的转换节点，对于尾码，随时可以转换，对于阶码，要在E-bias之后进行转换。
五、浮点数能表示的数
这是理解IEEE754的核心知识。理解深度学习中混合精度计算，需要对这一部分十分清楚。
我们使用5位的格式来举例说明。它包含1位符号位S，2位阶码（采用1位余码编码），两位尾数M(省略了“1.”)。
这种格式能表示的数值，如下表中的非零这一列所示：
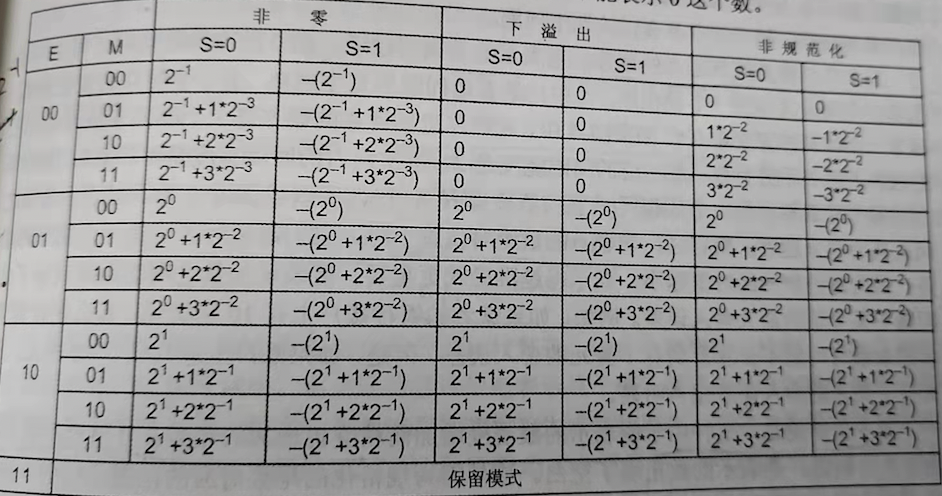
进一步，将能表示的数值画在数轴上。
注意，这里只画出了正数，负数和正数是对称的，没有画出来。
观察这些数值，可以得出五条结论：
1、能表示的数之间的主间隔取决于阶码位。
在上面的数轴上，可以看到有3个主间隔，这是因为阶码有2位。除掉保留模式，可以形成3个不同的幂。
2、每个间隔中能表示的数的个数取决于尾数位。如果尾数位2位，则在每个间隔内能表示4个数。一般而言，如果尾数位N位，则在每个间隔内能表示$2^N$个数。
如果一个要表示的值落在其中的一个间隔内，舍入后它就成为间隔内一个可表示的数。很显然，每个间隔内能表示的数的个数越多，在这个区间中我们要表示的数也越精确。因此，尾数的位数决定了表示的精度。
3、这种格式中不能表示0.
4、越靠近0的地方，可表示的数离得越近。向0的方向移动时，每个间隔是前一个间隔大小的一半。
换言之，当表示的数的绝对值越小时，它们越接近。这是一个良好的性质，因为这些数的绝对值越小，表示得越准确就更重要。能表示的数之间的距离决定了此间隔中某个值的最大舍入误差。
5、这种由于能表示的数密度增加而精度也增加的趋势在0附近不成立，因为在0附近，能表示的数出现了空白。这是因为规格化的尾数对应的范围已经把0排除掉了。这是一个严重的缺陷。
一般而言，在这种表示法中，如果尾数的位数为m，那么接近0的间隔内引入的误差要比下一个间隔内引入的误差大$2^m$倍。
六、表示0附近的数
一种办法是使用下溢出约定。即规定，当阶码为0时，对应的数是0，可参考上面的图中下溢出部分。
这种表示的代价是在0附近能表示的数之间出现了更大的空白。
实际上，IEEE754标准采用的是非规格化的方法。 这种方法在0附近时放宽了对规格化数的要求。当E=0时，不再假定尾数是1.M的形式，相反，假定它是0.M的形式。阶码所表示的值与之前的间隔仍相同。 这种方法能表示的数的范围如下所示：
从数轴上看，非规格化约定把在非零表示法中最后一个间隔内能表示的4个数分散开，用于弥补0附近的空白区域。
但这种方法也有代价。每当一个非规范化的数被生成和使用时，用硬件去实现往往会引入数千个时钟周期的延迟。
但是得益于制程技术的发展，2.0以上的cuda设备都支持非规范化的单精度运算。
总之，浮点格式和能表示的数的概念，这两个概念是理解精度的基础。浮点数表示法的精度取决于引入的最大误差，这种误差是要表示一个浮点数时，将它转为能表示的数而引入的误差。误差越小，精度越高。尾数的位数增加，可以提高浮点数表示法的精度。能表示的数增加一位尾数，可以将最大误差减少一半。
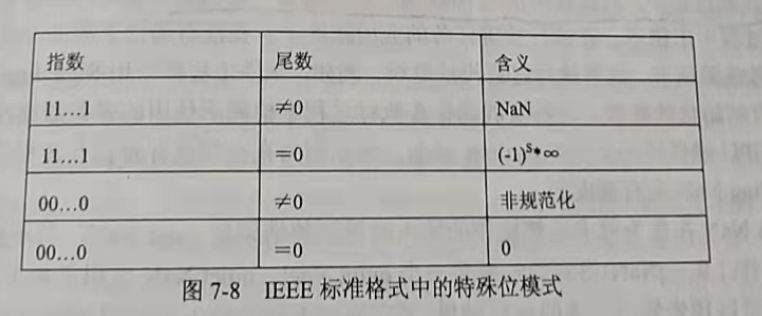
七、特殊值
IEEE标准中，使用一些特殊的位模式表示特殊值，如下图所示：
原创文章，转载请注明出处，否则拒绝转载！
本文链接：抬头看浏览器地址栏