链表判定环的入口和相交链表判定交点

2022-02-17

---

这两道题都有一个双指针的解法，而且要理解双指针解法，都需要画图进行一定的数学分析，所以放在一起做个对比分析，加深记忆。

链表判断环的入口

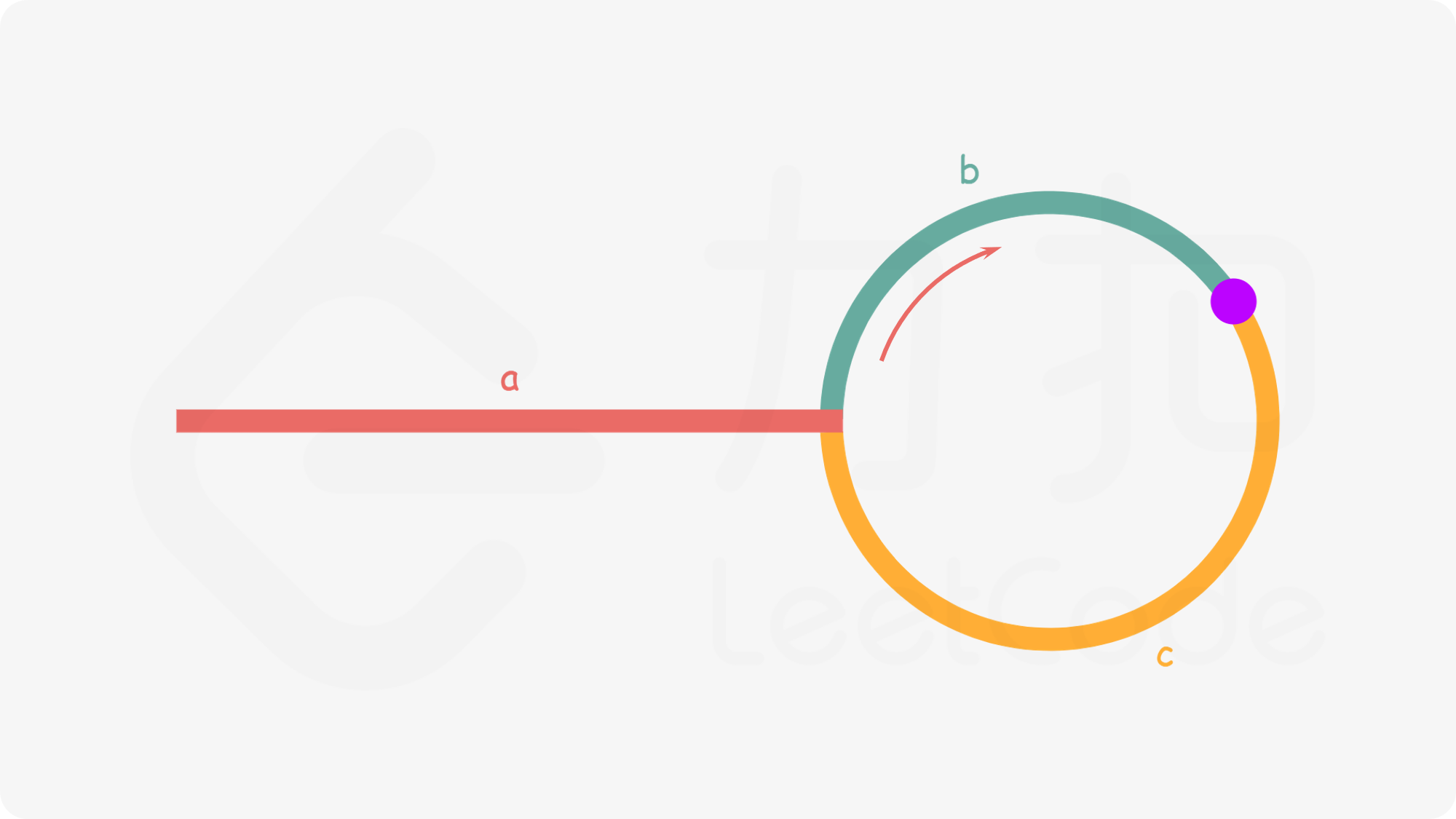
使用快慢指针，当二者在粉色点相遇时。快指针走的距离是：

a + b + n*(b+c)

慢指针走的距离是：

a + b

又因为快指针每次走两步，慢指针每次走一步，所以，快指针走的总距离是慢指针的总距离的2倍。

即：

a + b + n*(b+c) = 2*(a+b)

化简整理可得：

a = c + (n-1)(b+c)

翻译一下就是，从链表头部到入环点的距离等于从相遇点到入环点的距离加上n-1圈的环长。

根据这一发现，当发现slow与fast相遇时，可以再额外使用一个指针ptr，使它指向链表头部，随后，它和slow每次向后移动一个位置。最终，二者会在入环点相遇。

相交链表判定交点

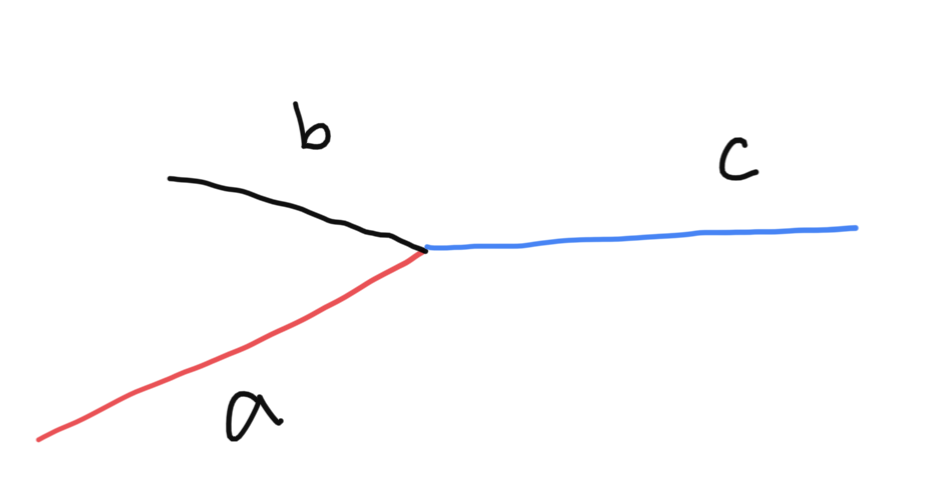
假设a+c是链表A，b+c是链表B。

起始时，两个指针都从头开始走，当一个指针到头后，转到另一个链表的头部，继续走。

不难发现，最终二者会在链表交点处相遇，它们走过的距离分别是：

b+c+a

a+c+b

显而易见，二者是相等的。

原创文章，转载请注明出处，否则拒绝转载！
本文链接：抬头看浏览器地址栏

---