最长回文字符串之马拉车算法

2022-02-09

马拉车算法用来在字符串中查找最长回文字符串。解法很妙，但是理解起来有点难。偶然看到一个外国人写的文章，解释的清晰易懂，这是学习的笔记。原文：这里

概述

Manacher算法帮助我们在给定的字符串中找到最长的回文子串。它的本质就是对暴力算法的优化。 这个思路在我的所有算法文章中一再强调了。暴力加优化和分类就是解决算法问题的两大神器。 它最大的作用是帮助我们迅速打开思路，尤其是面对陌生的问题时。

为了简单起见，我们先只处理有奇数个字符的字符串，关于偶数个字符的字符串，在文章最后会给出解法。我们的处理思路和暴力算法基本一致，那就是从左到右一个字符一个字符来处理这个字符串，寻找以当前处理的字符为中心的最长回文串，假设字符串的长度是N，那我们就在寻找到的N个最长回文串中取最长的就是答案了。

符号说明

这里的符号说明非常重要，请务必确保理解了每个符号的含义再继续往下看。很多中文的文章看起来头大，就是这几个符号的含义没说清楚。

我们约定，c是我们处理当前字符时，已经找到的最长的回文字符串的中心。l和r分别是这个最长的回文字符串的左界和右界，也就是最左边的字符索引和最右边的字符索引。现在，我们举个例子来理解c、l和r。

例子：”abacabacabb”

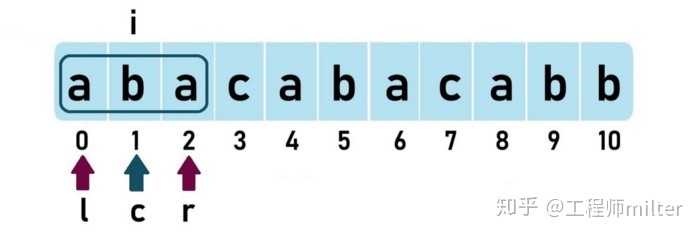
当从左到右一个字符一个字符计算时，我们用i表示当前正在处理的字符的索引，当i在索引1时，最长的回文字符串是 “aba”（长度=3）。

当i在索引5时，如下图所示：

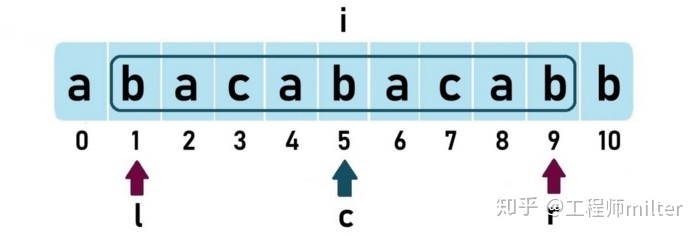
最长的回文字符串的答案是9，c、l、r的值如图中所示。

不难看出，c所代表的最长回文字符串

现在我们知道了c、l和r表示什么，为了下面算法的讲解更加自然，我们需要了解一个概念：镜像索引。

对于以c为中心的任何一个回文字符串来说 索引j关于c的镜像是j’，如下图所示：

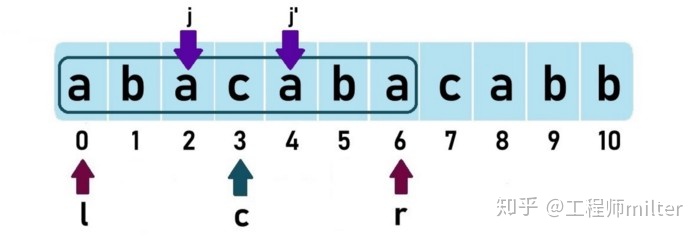
观察上图，不难得出下面的计算公式：

c - j = j' - c
#此时，j的镜像j':
j' = (2 * c) - j

算法思想

现在，我们已经定义了四个符号：c、r、l、i。i是我们正在处理的字符的索引。 c、r、l是我们的辅助数据。

我们先从整体上看一下算法的流程，然后详细解释每个步骤的并说明它的逻辑：

当我们处理到第i个字符时，我们的目标是找到以i为中心的最长的回文字符串，不妨称为iLongestPalindrome，并把这个它的长度的一半（即从i向左或向右的长度）存储在一个新的数组中，这个数组叫做P[]数组。

如果iLongestPalindrome的有边界超过了r，那么就将c更新为i，并同步更新l和r。

让我们继续用前面的例子来说明算法，如下图所示：

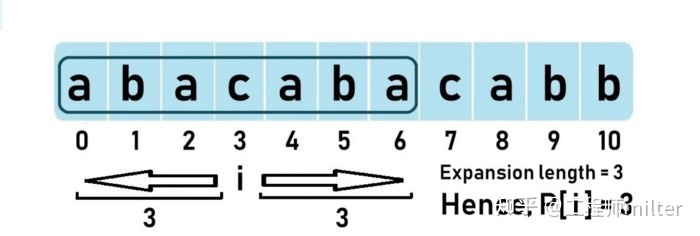
当i等于3时，通过向两侧延伸，不难计算出以i为中心的最长回文字符串是”abacaba”，此时，我们令P[i]=3，这是之前已经约定好的。

马拉车算法的核心作用就是：借助c、r、l提供的信息，在求P[i]的值时，不用傻傻的暴力向两侧延伸计算。

让以字符串 “abacaba”的P[]数组为例：

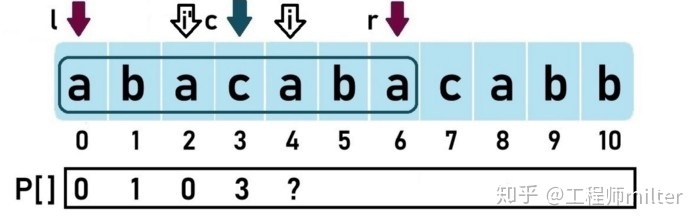
当i=4时，可以看出i<r。此时，我们不用天真地在i处向两侧扩展。我们可以先计算出肯定可以的以i为中心的最短回文字符串的长度，这样我们就可以在这个基础上通过继续向两侧扩展来计算P[i]，而不是从头开始做。

那要怎么做呢？

我们检查镜像索引i’。只要值i’ - P[i’]没有小于l（哎奥），我们就可以确定在i处肯定可以的最短回文字符串的长度是2P[i’] + 1，也就是说，至少可以从i向左右扩展P[i’]步。

这一点，一定要结合上面的图进行理解，不然就比较抽象。

请记住，我们只是在讨论最小可能的扩展长度，实际的可能扩展长度可能会更多，我们需要在此基础上继续扩展以得到最终的值。

在上图中，P[4]=P[2]=0。我们尝试借助已有的P数组，但就这个例子而言，很不幸，P[4]仍然是0。

这里有些特殊的情况我们还需要进一步考虑。

如果值i’ - P[i’] 跑到了l（哎奥）的左边，我们可以说i处最小的肯定可能扩展长度是r-i。

这个看起来也有点绕，必须用一个例子来说明一下，考察字符串”acacacb”。

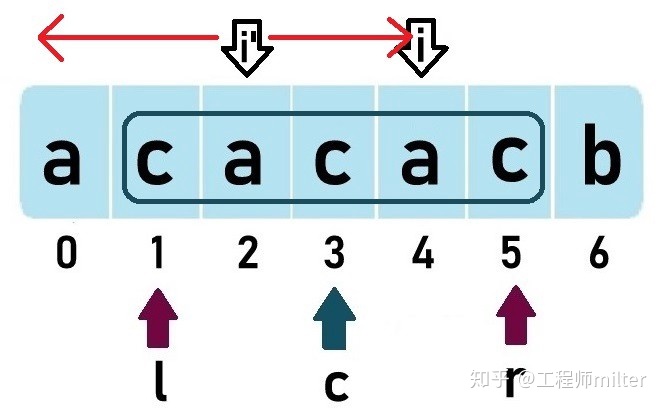
在这里，以i’为中心的回文字符串扩展到左界l之外。 所以，P[4]=5-4=1

你可能有疑问，为什么在这种情况下，以i为中心的最小确定回文字符串向右不能超过r呢？如果是这样的话，那以c为中心的最长回文字符串的长度也要增加，l和r也应该向两侧扩展，但实际上并没有。所以，P[i]=r-i。

(也就是说，如果在i处的回文字符串扩展到r之后，那么索引6处的字符应该是’a’。但如果这样的话，当前以c为中心的最长回文字符串就不是 “cacac “而是 “acacaca “了。)

上面的两种情况，用数学公式可以总结如下：

if(i < r){
  P[i] = Math.min(r - i, P[mirror]);
}

现在唯一剩下的就是在i左右P[i]位置继续向两侧扩展，所以我们从索引(P[i]+1)开始检查字符，并继续在i处扩展。

如果最后得到的结果，以i为中心的回文字符串的右边界超过了r，则将c更新为i，r更新为(i + P[i])。

按照上面的算法，我们就可以不断地填满数组P。2 * max(P) + 1就是我们要求的结果。

最后一点，在上面的解释中，我们取了一个奇数长度的字符串。因此，为了使这个算法成功，我们只需在每两个字符之间附加N+1个特殊字符（比如说’#’），以确保我们修改后的字符串总是奇数长度。

例子1: aba -> #a#b#a#。

例子2：Abba-> #a#b#b#a#。

代码实现

def  manachersAlgorithm(s):
    N = len(s)
    str = "#" + "#".join(s) + "#"
    leng = (2 * N) + 1
    P = [0] * leng
    c = 0 # stores the center of the longest palindromic substring until now
    r = 0 #stores the right boundary of the longest palindromic substring until now
    maxLen = 0
    for i in range(leng):
        # get mirror index of i
        mirror = (2 * c) - i
        
        # see if the mirror of i is expanding beyond the left boundary of current longest palindrome at center c
        # if it is, then take r - i as P[i]
        # else take P[mirror] as P[i]
        if i < r:
            P[i] = min(r - i, P[mirror])
        //expand at i
        a = i + (1 + P[i])
        b = i - (1 + P[i])
        while a < leng and b >= 0 and str[a] == str[b]: 
            P[i] += 1
            a += 1
            b -= 1
        
        #check if the expanded palindrome at i is expanding beyond the right boundary of current longest palindrome at center c
        #if it is, the new center is i
        if i + P[i] > r:
            c = i
            r = i + P[i]
            
            if P[i] > maxLen: #update maxlen
                maxLen = P[i]
            
        
    
    return maxLen

时间复杂度： O(N) 空间复杂度：O(N)